MATHEMATICAL MODELING OF INFECTIOUS DISEASES. Case Solution And Analysis, HBR Case Study Solution & Analysis of Harvard Case Studies

MATHEMATICAL MODELING OF INFECTIOUS DISEASES. Case Solution

Fixed population:

Mathematical Description of the SIR Model

Consider,

= number of individuals that can be infected per unit time by an infected patient

= number of individuals that one person comes in contact with per unit time

= number of total contacts with vulnerable people

= probability of infecting a vulnerable individual with whom an already infected patient is in contact with

= number of individuals infected by an already infectious person (suppose that all people in patients contact are vulnerable)

The equation below is the mathematical description of the SIR model defined in the ordinary differential equation (ODE) form.

Let’s replace (eq.4) into (eq.3) to find (eq.5)

Let be the probability that a person may recover at a time (from I to R compartment).

Variations of SIR Model

There are many variations of the SIR model, some of which are listed below:

The SIS model.
The SIRD model.
The MSIR model etc.

SIS model (Parshani, Carmi, & Havlin, 2010)includes the births and death,and it considers the case where there is no immunity after recovery. SIRS model is designed for scenarios where immunity only lasts for a very short period. MSIR model deals with the infants that can be born with an immunity to the infectious diseases.

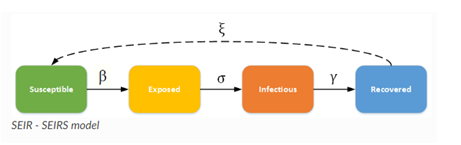
The SEIR or SEIRS Model

Many infectious diseases have a hidden or latent period. That means, an individual is infected during this phase but the symptoms take quitelong to occur. People going through the latent phase of the disease are not infectious. The SEIR model is designed for such diseases. SEIR stands for susceptible (S), exposed (E), infectious (I), and recovered (R). According to this mathematical model, each individual who gets the virus stays in the exposed (E) state of the model. In this stage virus of an infectious disease is supposed to be in an incubation state and it does not transmit to anyone else.

Mathematical Description of SEIR

Consider total pollution is N and and if SEIR is written for a closed population without births or deaths i.e. SEIR without any important dynamics then:

In the SIR model, supporting dynamics like birth and death can stand an epidemic or allow infectious diseases to spread.The mathematical model of SEIR with vital dynamic sis written as,

μ = birth dates

ν = death rates,

SEIRS orsusceptible (S), exposed (E), infectious (I), recovered (R), and susceptible (S) model is used to let recovered patients to return to a vulnerable state.

Mathematical Description of SEIRS

= rate of recovered individuals returned to the vulnerable or susceptible state due to the loss of immunity.

Vaccination Modeling

Vaccines are the best preventive tool in reducing mortality and illness rates among the population. However, health authorities find the implementation of vaccination policies challenging. To evaluate the various vaccination policies; modeling has become an integral part of the whole process (JA Bogaards, 2011). On the other hand, measuring the effectiveness of a vaccination program is also challenging and costly, which further raises the need for studies based on the whole population (Not feasible either). In this scenario, mathematical modeling creates a way out in measuring the effectiveness of indirect protection given through immunization. Two vaccines for rotavirus and HPV (Human Papilloma Virus) have been recently introduced to cater to diarrhea and cancer problems (C de Martel, 2012). Both vaccination programs have been implemented by many countries. Different transmission models have been constructed in order to attain a vast epidemiological effect and to understand the effects of the applied vaccination (C Atchison, 2010). To understand, HPV vaccination programs are taken as an example to understand the effectiveness of the immunization program. HPV leads to different complex issues, because it involves differences in sex outcomes, sexual transmissions, and adolescent vaccination. Different models have been studied in order to find out the optimal solution against HPV (IA Korostil, 2013). The models provided a better understanding of the effectiveness among vaccination models due to variation in various biological processes including virus stains, immunity, immunity, etc. Furthermore, modeling gave very informative insights regarding the questions, such as: the ages of target vaccination done of the key issues in HPV vaccination and catch-up policy related to the vaccination program.

Mass Vaccination Mathematics

It is a fact that diseases can no longer exist in the population if the number of individuals immune,exceeds the herd of immunity level. This means if a vaccination works and the number of the immune people increases then an infectious disease can be eliminated. For example:since the vaccination of smallpox was invented; the disease is now in control. Currently, polio vaccine drives are running under the WHO’s supervision to eliminate this disease.Scientists use mathematical modeling to calculate the critical immunization threshold, which indicates the smallest amount of the population that must be immunized at birth to eliminate a certain infections, completely........................

This is just a sample partial case solution. Please place the order on the website to order your own originally done case solution.

MATHEMATICAL MODELING OF INFECTIOUS DISEASES. Harvard Case Solution & Analysis